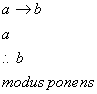



Eliasmith, Chris (unpublished). LT-Frame: A replacement for logical inference as a basis for human cognition. DRAFT. Dec. 1996.
Philosophy-Neuroscience-Psychology Program, Department of Philosophy, Washington University in St. Louis, Campus Box 1073, One Brookings Drive, St. Louis, MO 63130-4899, chris@twinearth.wustl.edu
A number of prominent psychologists have argued for the centrality of formal logic in human cognition. Included in this group are Lance Rips, Martin Braine, and Irvin Rock (see Thagard 1996). In particular, Irvin Rock (1977) is interested in defending the position that the process of perception is highly logic-like. However, he weakens his claim slightly by insisting that it is not necessarily the case that syllogistic reasoning is taking place in the brain, but rather that "thinking can be translated into a form of logical inference, as if it occurs in precisely that way, not that it does follow that form" (Rock 1977, p. 364). Of course, if thinking can be translated into logical inference, it must not break the rules of logical inference, so such a claim is still testable in regards to human cognition.
However, a number of early psychological experiments have clearly shown the great difficulty with which human subjects are able to perform some simple inferences. For example, in an experiment by Shapiro (reported in Wason and Johnson-Laird 1972) a group of college students was presented with four forms of logical arguments: modus ponens; modus tollens; denying the antecedent; and affirming the consequent. The first two are valid arguments, while the second two are logical fallacies. These arguments are respectively of the form:
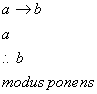



The results of this experiment were summarized by noting that: "The subjects certainly show a susceptibility to the fallacies, and a reliable difficulty in appreciating that modus tollendo tollens is valid" (Wason and Johnson-Laird 1972, p. 44).
It is interestingly odd that subjects who, according to Rock's theory, have basic perceptual mechanisms which "abhor" (Rock 1977, p. 367) logical contradiction seem to be unmoved by logical fallacies with which they are presented. It is true, of course, that the fallacies are being committed at a different 'level' of cognition. Nevertheless, if logic is fundamental to some types of cognition, and not others (especially where the former, in many ways, precedes the latter) a satisfactory cognitive theory must explain this inconsistency in human cognition. Rock (1977) does not attempt to address these sorts of difficulties with his theoretical approach.
In the remainder of this paper, I will present a different approach to modeling cognition which relies on learned transformations rather than logical inference. I will attempt to show how this theoretical framework is better able to explain both the functioning of the human perceptual system and the performance of human cognizers on tasks involving logical inference. I will begin the discussion by briefly describing the representational foundations of this new theoretical framework; which I will refer to as LT-Frame (Learned Transformation Framework). Subsequently, I will describe an example of human visual perception taken from Rock (1977) and show how this framework is better able to account for human performance on this tasks than is Rock's own. Finally, I will present evidence that this framework is also able to explain human performance (both good and bad) on logical inference tasks. Thus, I will propose a framework that is able to provide a unified explanation of human cognition that is not available under Rock's program.
The representational medium of LT-Frame is central to its ability to provide unified accounts of human cognition. The representations used in LT-Frame are called Holographic Reduced Representations or HRRs. HRRs are a particular form of distributed representation. The concept of distributed representation is a product of joint developments in the neurosciences and in connectionist work on recognition tasks (Churchland and Sejnowski 1992). Distributed representations have a number of important advantages over traditional forms of representation. Briefly, distributed representations:
The greatest shortcoming of distributed representations has been, until recently, their inability to capture complex structural relations. However, HRRs are both distributed, and structurally sensitive (Plate 1994). These representations are constructed, or encoded, using a form of vector multiplication called circular convolution and are related to the better-known tensor products of Smolensky (Smolensky 1990). Decoding of HRRs is performed using the approximate inverse of circular convolution, an operation called correlation (see appendix A for the algebraic details of these operations).
The HRR representations are "holographic" because the encoding and decoding operations (i.e. convolution and correlation) used to manipulate these complex distributed representations are the same as those which underlie explanations of holography (Borsellino and Poggio 1973). The convolution of two HRRs creates a third unique HRR which encodes the information present in the two previous HRRs. Importantly, this new HRR is not similar to either of its components, though the components may be retrieved through decoding the new HRR with the correlation operator. These operations are easiest to understand through a simple illustration. Let A, B and C be distributed, 3-dimensional HRR vectors. If C = A ƒ B (read: C equals A convolved with B) then, C # A B (read: C correlated with A approximately equals B) and C # B A (see figure 1).
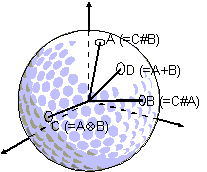
Figure 1. HRR operations depicted in three dimensions. Vector C is the circular convolution of vectors A and B. Vector D is the normalized superposition of A and B.
Along with convolution another operation, superposition, can be used to combine two HRR vectors. Superposition of two vectors simply results in their sum, and is written: D = A + B (see figure 1). Superimposing two vectors results in a vector which is very similar to the original two vectors but cannot provide a perfect reconstruction of the original vectors. This contrasts with convolution, in which the resulting vector is nothing like the original two vectors; in fact, the expected similarity of either of the original vectors to their convolution is zero (Plate 1994, p. 57). In both cases, some of the information in the original HRR vectors is lost in their combination. Hence, HRRs are considered 'reduced' representations. Upon encoding a new representation from a number of others, the new representation does not contain all of the information present prior to encoding. In other words, the new representation is noisy. Nevertheless, these representations are extremely effective at capturing complex relational information (Eliasmith and Thagard forthcoming). Furthermore, the noise occurring in HRRs seems to have a neurological counterpart (Andersen, personal comment).
When decoding an HRR vector the resultant vector must be recognized even though it is not expected to be identical to the vector that was encoded. The process of recognizing a vector is accomplished through use of another operator called the dot product and represented as 'ï'. The dot product of two vectors is the sum of the product of each of the corresponding elements of the vectors. For normalized vectors, the resulting scalar is equivalent to the length of one of the vectors projected on to the other. This relative length value can be used as a measure of the vectors' similarity. Because all of the vectors are normalized to the unit radius, we can use the dot product operation to determine the similarity of any two vectors.
A number of properties of HRRs make them promising candidates for modeling human cognition. First, HRRs are distributed representations. This means that they have all of the benefits associated with distributed representations.
Second, HRRs accommodate arbitrary variable binding through the use of convolution. Third, HRRs can effectively capture embedded structure (Plate, 1994; Eliasmith and Thagard, forthcoming). Fourth, unlike tensor products, and most other distributed representations which use vector multiplication, HRRs are fixed dimension vectors. Thus, convolving two three-dimensional vectors results in another three-dimensional vector -- not a six- or nine-dimensional vector. Consequently, HRRs are not subject to an explosion in the size of representations as the structures represented become more complex. This property also allows HRRs of various structural depths to be easily comparable to each other without "padding" the representation, as is necessary with tensor products. Fifth and finally, convolution can be implemented by a recurrent connectionist network (Plate, 1993). The potential for implementation in a recurrent network supports the neurological plausibility of HRRs. Though the extent of neurological realism of any such artificial neural networks may be disputed, it is indisputable that they are more neurologically realistic than either localist connectionist or symbolic models (Smolensky, 1995).
As an example of unconscious inference, Rock (1977) proposes the following example (p. 358):
Rock believes that the process of visual perception "is much like syllogistic reasoning...the premises and conclusions entail relations" (p. 359). As can be seen from this example, the conclusion of these sorts of syllogisms is a percept in the proximal mode (e.g., perceived angle).
There are two major drawbacks to Rock's account of visual perception in this example. First, Cooper and Shepard (1973) have shown that the amount of rotation of an object in the environment affects the time it takes to make decisions concerning orientation of the object (as in Thagard 1996). However, if perception of orientation is always a three step syllogism, it is not clear why the amount of rotation would have such an affect. Solution of the syllogism should take the same amount of time given that the premises are of the same complexity, only the values (i.e. 40o, 50o, and 90o) would vary.
Second, there is evidence that our perceptual systems do not provide accurate absolute measures of external stimuli. In particular, there is evidence that our vestibular system provides more accurate information concerning our orientation relative to the vertical the more upright we are, and fails completely at an angle of about 40o. Similarly, other sensory systems seem unable to provide 'veridical' information concerning the environment (Akins 1996). Thus, Rock is making, at the very least, controversial assumptions in claiming that absolute measures of orientation are readily available for the syllogistic reasoning process.
Using the LT-Frame, perception of orientation is understood in a much different, non-logical manner. Rather, on the basis of past experience, a general rotational transformation vector can be derived, and later applied to novel situations. Thus, given the vector representation of an image (for simplicity's sake, a point), say a = {0 1 0 0}, and the results of a right-rotation, b = {0 0 1 0}, it is possible to derive the vector which must be convolved with a to produce b as follows:
tright = a # b
In other words, the circular correlation of a with b provides the transformational vector for right rotations (i.e. tright). Similarly, the left-rotation transformation can be derived to give tleft. Once the transformation vectors have been formed, novel transformations can be produced. For instance, b circularly convolved with tright (i.e. b tright ) will produce the vector {0 0 0 1}. As well, the transformations can be performed one after the other to produce 'more distant' or 'further' rotations. Thus, b tleft tleft will produce the vector {1 0 0 0} (see appendix B for details).
Notably, the LT-Frame avoids both of the short-comings of the unconscious inference framework. First, the amount of rotation of an object will affect the time it takes to perform the transformation since more transformations will have to be applied to the representation of the object the farther it is from the vertical. This property fits well with experimental evidence (Kosslyn 1994). Second, the transformation that is applied is based on the past experience of the perceiver. Thus, we do not need to assume that the perceptual system provides accurate absolute measures of object orientation, only that it is consistent.
As noted in the introduction, it seems odd that though, according to Rock's theory, our perceptual system is fundamentally logical evidence at the psychological level shows that people have great difficulty with simple logical operations. It is not clear how Rock would explain this apparent inconsistency. Whatever the explanation was, it would likely introduce notions foreign to syllogistic logic, and render Rock's overall theory of cognition far more complex, and perhaps result in a piecemeal explanation of the data.
In contrast, the LT-Frame is able to account for both perceptual and psychological phenomena. The previous section discussed the former. This section will address how the LT-Frame accounts for human logical performance -- both its strengths and weaknesses. Together, these sections demonstrate the ability of the LT-Frame to provide a unified account of human cognition.
Unlike the four dimensional vector used in the rotational simulations, a 4096 dimensional vector is used to perform the logical operations. To encode the logical sentence "a b" the following HRR is constructed (see appendix C, input):
C1 = rel implies + ante a + cnsq b
This encodes that the relation between the antecedent and the consequent is one of implication. This is a general propositional encoding scheme which has been used successfully to perform complex analogical mappings (see Eliasmith and Thagard forthcoming). Once the simple logical sentence has been encoded, it is necessary to construct transformations that will change the sentence into one which can be decoded as required (e.g. to perform modus ponens). For example, a modus ponens transformation is:
tmp1 = ante # (cnsq # C1)
When convolved with C1, this transformation will replace the ante designator with whatever is in the cnsq position of C1. So, letting C2 = C1 tmp1, we can imagine the transformation to have made C2 as:
C2 = rel implies + b a
Thus, upon correlating C2 with a (the antecedent of the conditional), the 'answer' is b. Thus, when the transformation is applied to C1, the correlation of the result with the antecedent of C1 will be approximately equal to the consequent of C1. This is how the system performs modus ponens on any sentence of the form "a b".
For modus tollens, another transformation must be constructed (tmt1) such that correlation of ~b with C1 tmt1 will be approximately equal to ~a. Appendix C provides two such transformations. Notice that being able to provide multiple ways of performing the same logical inference is a possible means of accounting for individual differences in performance on this task. In this case, tmt1 seems to be a less reliable transformation for perform modus tollens than tmt2. As well, the modus tollens transformation is far more complex than that necessary for performing modus tollens. This difference fits well with the psychological data which shows that people have far more difficulty correctly performing modus tollens than modus ponens (Wason and Johnson-Laird 1972).
Also, as appendix C demonstrates, these transformations provide a means of explaining the tendency subjects have to accept logical fallacies (in particular affirming the consequent and denying the antecedent). Since these transformations can also be used with an invalid query (e.g., "a b, b, ?"), it is possible to see how fallacies arise. The reason that fallacies are not always reported as valid would thus be due to learning the form of a valid query.
Though the results of both the perceptual and logical examples discussed are preliminary, they provide a promising route for providing a unified account of human cognition. As well, these applications of the LT-Frame for explaining cognition fit better with empirical data than the unconscious inference framework proposed by Rock (1977) and others. Speech perception.
Consider a set E of elements which are holographic reduced representations (HRRs). A member of E is an n-dimensional vector whose contents may represent an image, a proposition, a concept, etc. The prima facie similarity of two vectors is captured by their dot product. The operations necessary to encode and decode HRRs can be understood as follows:
Let be the space of item vectors in n-dimensions,
and let
be the space of stored vectors in n-dimensions.
Let
be the encoding operation (circular convolution),
be the decoding operation (circular correlation), and
be the superposition operation (addition). These three operations make it possible to store any relations necessary for generating the network of relations amongst elements of E.
The circular convolution operation ƒ is often referred to simply as convolution and consists of the following operations for c = a ƒ b where a, b, and c are n-dimensional vectors:
co = aobo + anb1 + an-1b2 + ... + a1bn
c1 = a1bo + aob1 + anb2 + ... + a2bn
cn = anbo + an-1b1 + ... + aobn
or
for j=0 to n-1 (subscripts are modulo-n)
This operation can be represented as:
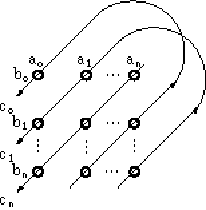
Figure 2. Visual representation of circular convolution (adapted from Plate (1994)).
Similarly, the circular correlation operation # is often referred to simply as correlation and consists of the following operations for d = a # c:
do = aoco + a1c1 + ... + ancn
d1 = anco + aoc1 + ... + an-1cn
dn = a1co + a2c1 + ... + aocn
or
for j=0 to n-1 (subscripts are modulo-n)
This operation can be represented as:
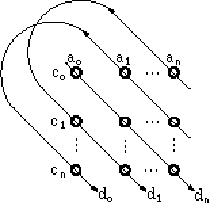
Figure 3. Visual representation of circular correlation (adapted from Plate (1994)).
Notably, the correlation of two vectors a # c can be written as a* ƒ c where a* is the approximate inverse of a which is defined as:
Let
a = {ao, a1, ..., an}
then
a* = {ao, an, ..., a1}
Though the exact inverse, a-1, could be used to decode a ƒ c exactly, this process results in a lower signal-to-noise ratio in the retrieved vectors in most instances.
These simulations were performed using PowerMac 8500. The software was written by Tony Plate in C. I ported the software to the Mac environment using Metrowerks Code Warrior.
# Very simple simulation of visual rotation.
#The vectors (only a and b need be specified, but
#entering them all clarifies the output)
a = {1 0 0 0}
b = {0 1 0 0}
c = {0 0 1 0}
d = {0 0 0 1}
#Calculating the transformations
t_left = <b'*a>
t_right = <a'*b>
#Storing the possible answers in clean up memory
store(mem, a, b, c, d)
#Provide the top two answers
match.capacity = 2
To understand the output, take the following as an example:
1. > match(mem, a*t_left)
d 1
c 1.22e-16
In this case, the transformation a tleft is matched to clean up memory to determine which know vector it most closely matches. The top two answers are displayed, with the similarity measure provided to the left of the vector's name. Therefore, vector d = {1 0 0 0} is the best match for this transformation with a similarity of 1 (i.e. 100%). The following examples can be understood in the same manner.
2. > match(mem, a*t_right)
b 1
a 1.22e-16
3. > match(mem, b*t_right*t_right*t_right)
a 1
b 3.67e-16
4. > match(mem, d*t_right)
a 1
b 1.22e-16
5. > match(mem, c*t_right*t_left)
c 1
b 2.45e-16
These simulations were performed using PowerMac 8500. The software was written by Tony Plate in C. I ported the software to the Mac environment using Metrowerks Code Warrior.
#Logical inference using TL-Frame
#Generate the vectors needed to encode the logical statements
a = randvec()
b = randvec()
not = randvec()
rel = randvec()
impl = randvec()
ante = randvec()
cnsq = randvec()
#Encode the negation of a and b
not_a = <not * a>
not_b = <not * b>
#Encode a->b
c1 = <rel * impl + ante*a + cnsq*b>
#Store the vectors in clean up memory
store(mem, a, b, impl, ante, cnsq, c1, not_a, not_b)
store(mem, not)
#Show the 2 best answers to any query
match.capacity = 2
#MODUS PONENS
#Construct the modus ponens transformation
tmp1 = <ante'*<cnsq'*c1>>
# The transformation can also be done as follows (they are the same)
tmp2 = <cnsq'*<ante'*c1>>
#MODUS TOLLENS
#Version 1 using the modus ponens transformation
t1 = <<ante'*c1>'*cnsq' * c1 * not>
t2 = <<cnsq'*c1>' * ante'*c1 * not>
t3 = <t1+t2>
tmp3 = <ante'*<cnsq'*<c1*t3>>>
tmt1= <t3*tmp3>
#same as above in one step
tmt2 = <<<<<ante'*c1>'*cnsq' * c1 * not> + <<cnsq'*c1>' * ante'*c1 * not>> * tmp2>>>>>*<ante'*<cnsq'*<c1 * <<<<ante'*c1>'*cnsq' * c1 * not> + <<cnsq'*c1>' * ante'*c1 * not>> * tmp2>>>>>>
#Version 2, not using the modus ponens transformation
t5 = <<ante'*c1>' * ante'*c1 * not>
t6 = <ante'*cnsq'*c1*not>
tmt3 = <t5*t6>
#same as above in one step
tmt4 = <<<ante'*c1>' * ante'*c1 * not> * <ante'*cnsq'*c1*not>>
# Perform the Transformations
c2 = <c1*tmp1>
c3 = <c1*tmt1>
c4 = <c1*tmt3>
Note that '* is the same as #, i.e. the operator for circular correlation. Thus, the modus ponens example shows that the best match to C2 # a is b. C2 is equal to C1 convolved with the operator tmp1 (i.e. C2 tmp1). Thus it is the transformed version of the proposition "a implies b" which will perform modus ponens upon correlation with a. The output can be similarly understood for the modus tollens and other examples.
> match(mem, a'*c2)
b 0.770
???
Transformation 1
> match(mem, not_b'*c3)
not_a 0.109
c1 0.104
Transformation 2
> match(mem, not_b'*c4)
not_a 0.279
not 0.0719
> match(mem, b'*c2)
a 0.607
???
Transformation 1
> match(mem, not_a'*c3)
not_b 0.109
ante 0.0758
Transformation 2
> match(mem, not_a'*c4)
not_b 0.279
not_a 0.223
Akins, K. (1996). Of sensory systems and the "aboutness" of mental states. Journal of Philosophy: 337-72.
Borsellino, A. and T. Poggio (1973). Convolution and correlation algebras. Kybernetik 13: 113-122.
Churchland, P. M. (1992). A feed-forward network for fast stereo vision with a movable fusion plane. Android Epistemology: Proceedings of the 2nd International Workshop on Human and Machine Cognition, Cambridge, MA, AAAI Press/MIT Press.
Churchland, P. S. and T. Sejnowski (1992). The computational brain. Cambridge, MA, MIT Press.
Eliasmith, C. and P. Thagard (forthcoming). Integrating structure and meaning: A distributed model of analogical mapping. Psychological Review under review.
Hinton, G. E. (1986). Learning distributed representations of concepts. Eighth Conference of the Cognitive Science Society, Lawrence Erlbaum Associates.
Kosslyn, S. (1994). Image and brain: The resolution of the imagery debate. Cambridge, MA, The MIT Press.
Lazzaro, J. and C. Mead (1989). A silicon model of auditory localization. Neural Computation 1: 47-57.
Plate, T. A. (1994). Distributed representations and nested compositional structure, PhD Thesis. University of Toronto.
Qian, N. and T. J. Sejnowski (1988). Learning to solve random-dot seterograms of dense and transparent surfaces with recurrent backpropagation. Connectionist Models Summer School, San Mateo, Morgan Kaufmann Publishers.
Rock, I. (1977). In defense of unconscious inference. Stability and constancy in visual perception. W. Epstein. New York, NY, Wiley.
Skarda, C. A. and W. J. Freeman (1987). How brains make chaos in order to make sense of the world. Behavioral and Brain Sciences 10: 161-195.
Smolensky, P. (1990). Tensor product variable binding and the representation of symbolic structures in connectionist systems. Artificial Intelligence 46: 159-217.
Smolensky, P. (1995). Computational models of mind. A companion to the philosophy of mind. S. Guttenplan. Cambridge, MA, Blackwell.
Thagard, P. (1996). Mind: Introduction to cognitive science. Cambridge, MA, MIT Press.
Wason, P. and P. Johnson-Laird (1972). Psychology of reasoning: Structure and content. Cambridge, MA, Harvard University Press.